Fun with Stats
Apropos a discussion on the effects of the Bush tax cut at FactCheck.org and Begging to Differ, Chris Lawrence gives us a review of two often-confused measures of central tendency, the mean and the median.* It’s rather common practice for sides in a debate to pick the one that best fits their argument. The press typically doesn’t help matters by using the word “average,” usually understood to be a synonym for arithmetic mean, carelessly.
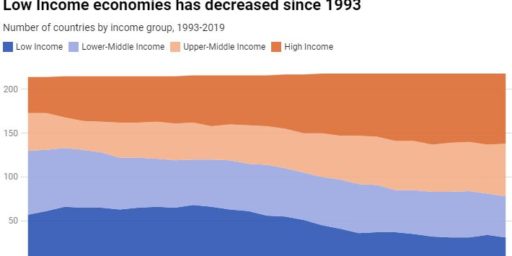
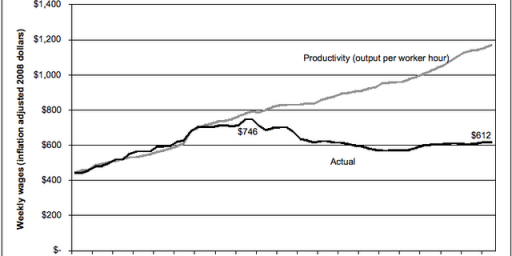
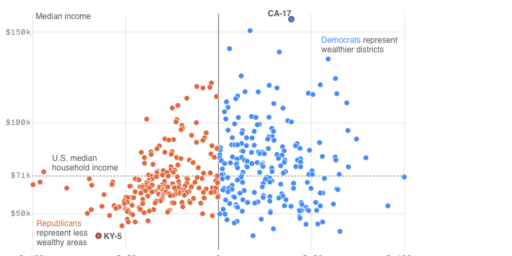
I agree with Chris that the median is almost always a more useful indicator, since the mean can be skewed by huge figures even in a large sample. This is especially true for income and similar economic variables, which are bounded at the bottom but not at the top. Even with something as large as the U.S. population, a handful of billionaires can skew the stats–whereas even the poorest of the poor have only a miniscule effect.
*Typically, he makes no mention of the mode, the nearly useless third measure.



I mentioned the mode in the second (and horribly long) footnote. I didn’t talk about geometric or harmonic means, though, which also have their purposes (generally as more robust alternatives to the arithmetic mean when you have outliers). And modes have their uses, but mostly as descriptive things (“I have a bimodal distribution” and such); also, the classification accuracy of some limited-dependent variable models can be measured versus preponderance of the mode.
I think the reason why the arithmetic mean is popular is (a) it’s the one people learn first, and (b) it’s probably the easiest to figure out, particularly if you don’t have a computer. And they work great when things are close to normally distributed or you can do the old asymptotic-handwave routine.
Although Statistics has always interested me, I’m pretty much stuck in the “average” crowd. And you definitely got me with the “asymptotic-handwave routine” phrase, Chris. I just have to nod my head and say, “He must know what he’s talking about, ’cause I sure as hell don’t!”
Oh, and to the point at hand: I agree with FactCheck.org on this point. Which figure is more meaningful, the average tax cut or the tax cut for the average taxpayer? It seems to me that the median is more realistic, but then again, it depends on what point you’re trying to get across. It isn’t “wrong” to use either figure, although it would probably be wrong to try to suppress one of them.
Where I differ with FactCheck.org is their insistence on including people who don’t pay income taxes in the calculations. While that can provide useful information, I’m personally not interested in giving an income tax cut to people who don’t pay income taxes, so the more meaningful figures, to me, are those that include only people who actually got a tax cut.
The payroll taxes are a separate issue, and being a bit anal-retentive myself, I think it would be better if the President would always say “income tax cuts” instead of “tax cuts,” and similar formulations. With his more stereotypical Texas cavalier approach to speech, though, I think that’s unlikely to happen. (I’m a Texan, by the way, so I’m speaking about my own group, thankyouverymuch.)
—