I Don’t Think That Word Means…
…what you think it means. An alternative title could be, Steve gets nitpicky. Mark Chu-Carroll at Good Math, Bad Math usually does a bang-up job of exposing bad math. His posts on evolutionary algorithms and how the criticisms of them are pretty good in that they make such subjects more accessible to non-experts. However, every now and then he slips, and this is one such example.
In this post Mark is taking on AIDS/HIV denialists and basically he is right save for one mistake that I wish he would take a few minutes to fix.
Anyway – for illustratory purposes, let me take the statement about probability and numbers of sexual contact, and try to rephrase it in a non-misleading way.
“The probability of acquiring HIV via a single act of unprotected sexual intercourse is approximately 1 in 1000. Therefore, one would expect 1000 unprotected sexual contacts with HIV positive individuals for each sexual transmission of HIV.”
Now… That’s an honest restatement. The next step of their reasoning is shoddy nonsense. It’s classic faulty Bayesian reasoning: 1/1000 is the probability of transmission via a single unprotected sexual contact; 1/250 is the probability of an individual being HIV positive; therefore, the probability of transmission by a single sexual contact with an individual with unknown HIV status is (1/1000)×(1/250). But remember the Bayesian rule: P(X and Y) = P(X)×P(Y) only if X and Y are independent.
Bayesian reasoning? I don’t think so. The “rule” P(X and Y) = P(X)×P(Y) only if X and Y are independent isn’t the “Bayesian rule”, it is the definition of independent events. For example, we have Robert Ash’s Real Analysis and Probability (page 204),
5.3.1 Definition Two events A and B are independent iff
The “iff” means “if and only if” which also means we could switch things around to read,
5.3.1 Definition
,
iff Two events A and B are independent.
Bayes theorem, a.k.a. Bayes rules, is
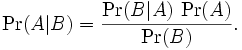
Clearly this is not the same as the above definition. Also, it is clear that Mark Chu-Carroll’s reference to “Bayesian reasoning” and “Bayesian rule” is bad math. However, this error is not fatal to Mark Chu-Carroll’s argument that AIDS/HIV denialists are wrong on the number of sexual contacts for aquiring AIDS/HIV. While he uses the wrong terms and possibly confuses some readers, the basic point that sexual behavior in a population is not independent is correct. After all, HIV is much more common amongst certain sub-populations within the population.






Pedant!
Guilty…at least on this topic. This is one of those things that just annoys me to the point where I can’t ignore it.
The problem here is not that the two variables aren’t independent, but that they are simply not the right variables. We don’t select our partners from a random pool where 1 in 250 is HIV-positive. There are a vast number of subgroups from which most of us choose not to seek partners: the retarded, the mentally ill, the physically handicapped, the congenitally deformed. Since the incidence of sex among these subgroups is thus artificially low, the incidence of HIV is also artificially low, driving the incidence across the population drastically downward.
Furthermore, we don’t select a new partner for each and every sexual contact: we tend to keep the same one as long as possible before switching. The argument is just plain broken out of the gate, no matter what the numbers happen to be.
Which basically says that the two variables are not independent. If we selected partners randomly then the two variables would be independent. But we don’t as you note above.