New Horizons Sends Back Images Of Ultima Thule
Three and a half years after its flyby of Pluto, the New Horizons spacecraft has reached the furthest distant object ever visited by a man-made craft.
It was roughly three and a half years ago that NASA’s New Horizons spacecraft flew by Pluto and provided the world with the clearest photos yet of the Dwarf Planet that orbits the Sun beyond the orbit of Neptune. The mission, which took nine years to reach its distant destination even though it was flying at speeds somewhat faster than many of the interplanetary unmanned craft that have been sent into space in the pace, was considered an outstanding success, but the little craft hasn’t stopped doing its job. Since visiting Pluto, New Horizons has had encounters with several trans-Plutonian objects, the most recent being Ultima Thule, which is so far the most-distant object encountered by a man-made craft:
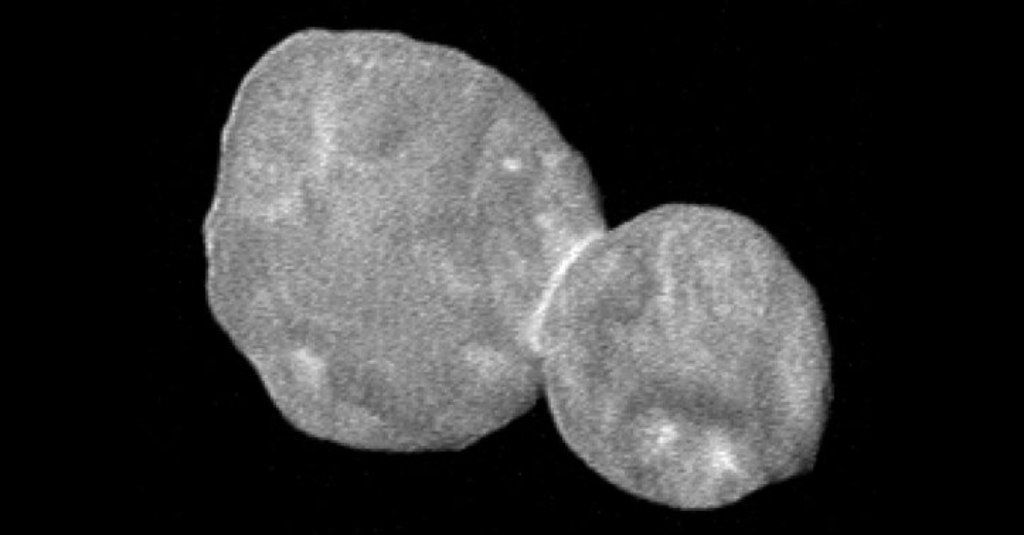
LAUREL, Md. — Ultima Thule, an icy world 4 billion miles from the sun, looks like a big snowman.
At a news conference on Wednesday, scientists working with NASA’s New Horizons mission released several images that the spacecraft took as it flew by on Tuesday, New Year’s Day.
Planetary scientists have never before seen a close-up of a body like Ultima Thule. It is likely a fragment that coalesced more than 4.5 billion years ago and which has remained in the deep freeze of the solar system’s Kuiper belt ever since.
If it is indeed a pristine planetesimal, a building block of the planets, studying it will offer clues to how Earth and its neighbors formed.
On Tuesday, scientists released a blurry picture of this small world, also known by its official designation 2014 MU69, taken before the flyby from a distance of half a million miles. It sort of looked like a fuzzy bowling pin then.
“That was so 2018,” Dr. Stern joked.
Now, much more has come into focus.
The scientists now say with confidence that Ultima Thule long ago was what they call a “contact binary.”
“Two completely separate objects that are now joined together,” said S. Alan Stern, the principal investigator for the mission.
It consists of two almost spherical lobes, one with about three times the volume of the other. To tell them apart, they named the larger one Ultima and the smaller one Thule. “Being scientists, we are not all that creative with words,” Dr. Stern said.
Such contact binaries appear to be common in the outer solar system, but, Dr. Stern said, “This is the first object that we can clearly tell was born this way,”
By contrast, he suggested, scientists did not know for sure whether other two-lobe bodies — most notably the rubber ducky-like Comet 67P/Churyumov-Gerasimenko — were two objects that came together or one larger body that had eroded into its current shape.
A contact binary fits with some theories of how the planets formed — that clouds of pebbles clumped together into larger lobe-size bodies, and then these two lobes gently bumped into each other and stuck.
“It’s actually gratifying to see these almost perfectly formed contact binaries in their native habitats,” said Jeffrey M. Moore, the leader of the mission’s geology and geophysics team.
In at least the general outlines, he added, “our ideas of how these things form seem to be somewhat vindicated by these observations.”
He said that the two lobes must have hit at very low speeds, a few miles per hour at most. Dr. Moore said that the mottled appearance of the surface with dark streaks were suggestive of hills and ridges. As yet, there are no obvious craters visible.
“We see no unambiguous evidence,” Dr. Moore said. “I’d be surprised if there are not at least a few.”
Because these images were taken with the sun directly behind the spacecraft, there are no shadows to highlight the topography
Color images show that Ultima Thule is reddish. A ring of brighter, less reddish material circles the connection between the two lobes, possibly loose material that rolled down and piled up at the bottom of the slopes.
The details of the shape conclusively answer the mystery of why New Horizons did not detect variations in Ultima Thule’s brightness as it approached. Typically, an irregularly shaped object will have a rhythmic pattern of brightening and dimming as it rotates. But here, the spacecraft was looking down at one of the poles, so essentially the same side of Ultima Thule was facing the spacecraft the entire time.
The first batch of science data from the flyby arrived on Earth on Tuesday afternoon. More than 100 scientists, including Heidi B. Hammel, a planetary scientist and a media liaison for the science team, gathered in the evening for a look.
“Everybody was there,” Dr. Hammel said in an interview. “They all wanted to see it. The picture goes up and everybody applauds and cheers. Immediately, the chatter starts.”
Ultima Thule was first discovered very recently, in June 2014 by astronomers using the Hubble Space Telescope who were looking for new targets for New Horizons in the wake of its flyby of Pluto. Technically, Ultima Thule is only a nickname for the object and its official name will eventually be assigned pursuant to the guidelines of the International Astronomical Union, although one hopes that its current nom de guerre becomes official in no small part because it sounds like someplace that might exist in the Star Wars universe. In reality, the nickame comes from Latin and roughly translates into “farthest Thule,” meaning an object lying the furthest from the known world. In any case, whatever the object is ultimately called, the fact that we’re now flying a craft by it is really one of those extraordinary accomplishments that probably don’t get the attention they deserve because they aren’t as sexy as the manned space program. In terms of actual science, though, it’s rather clear that the unmanned probes that have been sent into the Solar System, largely by the United States, have been far more important to the expansion of human knowledge than the manned program has been. At some point, perhaps, a manned mission will do what Pioneer, Voyager, New Horizons, and other missions have done, and more, but for now these little robots are our best way to find out more about the universe and they’re doing a fantastic job.
The object itself has an orbital period of 298 years, meaning that it takes nearly 300 years for Ultima Thule to make a complete orbit around the Sun. For perspective’s sake, this means it was last in its current position in roughly 1718 when the American colonies were still beginning to form on the East Coast of North America, George I was King of Great Britain, Czar Peter the Great ruled Russia, and Louis XV ruled France. It won’t be back in this position again until 2318. In terms of distance, it lies roughly 42.5 to 44.5 Astronomical Units from Earth, a distance that varies due to the fact that its orbit is not consistent in the manner that most planets are. No doubt, there will be more data and more pictures in the coming days. Even these initial images, which took more than twelve hours to make the journey from the craft to Earth and be properly processed, are amazing though. Nicely done, New Horizons. Nicely done.





The photo is a cautionary tale: be careful when making pancakes to allow enough separation, otherwise your pancakes will run together.
It’s less than 30 miles in length. That’s remarkably small for an object that can be detected from such a distance.
@Kylopod: it took the Hubble to spot it, it’s very faint.
https://en.m.wikipedia.org/wiki/(486958)_2014_MU69
Now I have to rant.
What the Curiosity rover has done over years, a team of human scientists would have accomplished in days. Albeit at a much, much, much, higher price tag, possibly including a few lives (see Challenger, Columbia, Apollo I, and one Soyuz mission).
Access to space is about cost. It costs a lot less to send a robot probe anywhere than it costs to send people. The longer the trip, the cheaper the probe is. This is the same principle that tells you it’s cheaper to ship cargo than passengers, and for much the same reasons.
The manned program does attract attention, but only for a little while. Once the novelty wears off, people kind of stop caring. Apollo XI was a big media event. Apollo XII not so much.
Fact is there is no good reason to send people to Mars, or the asteroids, or even to the Moon again, solely for exploration. Robots can do it more cheaply, and there’s no big rush to learn the secrets of the various parts of the Solar System. If and when there’s money to be made off space travel, that’s when we’ll see large numbers of people go into space.
@Kathy:
I forget where I saw this, some YouTube thing no doubt. But it was pointed out that while homo neanderthalensis had as big a brain and seemed about as advanced as homo sapiens, Neanderthal man stuck close to home and did not go adventuring. H. Sap by contrast does obviously stupid things like wake up one morning and think, “Hey, I wonder what’s way the hell out there on the ocean? I don’t have a compass, or even know the concept of north or south, but hey, I can hollow out a tree!”
H. sap wiped H. neanderthal out completely, retaining a few scraps of their DNA and nothing else. It may be that we have an instinct to explore, to seek out new life, and new civilizations, to boldly go… It may be an evolutionary thing that contributed to our success as a species. No human in the story means no interest from the vast majority of people. 95% of people don’t give a single sht about knowing the composition of Mars rocks. Put a human in the story and it attracts a great deal more attention.
You’re not fooling me! This is a sonogram of The Thing before he was born!
@Michael Reynolds:
Oh, please. This is just so transparently another of Trump’s Big Lies. A little Vaseline on the lens, gray shade lighting, and some incompetently (Isn’t everything he does??) poured pancakes.
It will be covered for days here at OTB and a Blue Ribbon panel of experts has been assembled for tonight on CNN to discuss whether its an impeachable offense…………
@Kylopod: Especially since it’s about as reflective as garden dirt and illuminated by a Sun that’s 1,900 times dimmer than it is here on Earth.
Most amazing to me is how we can launch a probe four billion miles to intercept an object 20 miles in size and get it exactly where we want it.
REPUBLICAN President Pud is too dumb to have anything to do with this.
@Michael Reynolds: Are you deliberately trying to get someone to bring up the Douglas Adams quote?
“For instance, on the planet Earth, man had always assumed that he was more intelligent than dolphins because he had achieved so much–the wheel, New York, wars and so on–whilst all the dolphins had ever done was muck about in the water having a good time. But conversely, the dolphins had always believed that they were far more intelligent than man–for precisely the same reasons.”
@Michael Reynolds:
I haven’t come across that one before. But Neanderthals ranged through almost all of Europe and well into central Asia and the Middle East. Hardly stationary.
Hunter-gatherer humans moved farther afield as they ran out of food and went looking for more. I’ve no idea if they even knew they were venturing into parts unknown. I suppose they must have. it’s not as though a band of hunter-gatherers simply roams aimlessly.
The invention of stone tools and fire would have given our ancestors an edge over other species, and thus let them increase in numbers. This would perforce require some of them to look for better pickings elsewhere (and in a way we haven’t yet stopped).
Anyway, you can motivate people to move when there’s no room for them at home. Or when they can make a fortune elsewhere. Thus far, profits in space remain close to home: communication satellites, earth resources satellites, weather satellites, GPS satellites, and other satellites.
As Mikey notes,
I would add to that that if my calendar is correct, we didn’t even know about Ultima Thule (discovered by Hubble in 2014) when we launched New Horizons (in 2006). As I understand (vaguely) how these things are done, we have a very limited ability to change its trajectory so that we can sling it around an object like Pluto to “aim” it where we think Ultima will be in 3 years and get this close.
Try that in the next person who tells you physics is just a theory.
@Joe:
I’ll let you in on something more impressive:
There is a formula to calculate the trajectory of any two objects as determined by their respective gravity and starting conditions. There is no formula that does the same for three or more bodies.
So what you do is calculate the gravitational effects of all other major bodies involved, and add them up to modify the original two body solution. This does not involve any kind of exotic math, but there are a lot of gravitational sources mucking things up.
I don’t know what sources have what effects on Pluto, Ultima Thulle, and New horizons. But since the probe left from Earth and slung past Jupiter, those two need to be accounted for.
All probes launched so far receive most of their velocity from the launch vehicle, usually the uppermost stage of a rocket. They carry some fuel and oxidizer, and have small engines as well, because despite all calculations there might be a need to maneuver or make course corrections. But every gram of fuel and engine means one fewer gram for instruments or nuclear batteries (solar panels are worse than useless that far from the Sun). On the other hand, every extra gram of fuel adds to the certainty of a successful mission. Imagine flying past Pluto a million miles farther away than planned because you lacked enough fuel for a course correction.
It’s a complicated problem.
Try that on the next person who tells you physics is just a theory.
Evolution is just a theory.
How many times have you heard that?
I tell those deniers that electricity is just a theory and that they should stick their finger in a light socket to test what a good theory it is!
If that doesn’t convince them I tell them that gravity is just a theory and that they should jump out of a tall tree to test what a good theory it is!
If that doesn’t work all that’s left to say to them is Genesis isn’t even a theory. It’s a Fairy Tale!
@Kathy: At this year’s ISDC (International Space Development Conference) there was someone from JPL giving a talk about the end of the Cassini mission and all the gravity assists they had used….
(Which is why the one big stinking howler in “The Martian” is the silly “NASA doesn’t immediately think of gravity assists!” It’s like assuming a cardiologist not recognising symptoms of a heart attack….)
@Mister Bluster:
And there is this photo…
Gravity assists are amazing, but they take time.
After the Challenger accident, several payloads designed for the Shuttle were changed to solid fuels only. This impacted the Galileo probe, to the point they had to calculate gravity assists at Venus, and twice at Earth.
The Voyager probes benefited from a planetary alignment. So that Voyager 2 could pick up assists from Jupiter, Saturn, and Uranus, studying each in turn, and finally flying past Neptune.
That was when NASA could afford (or needed) to launch two probes per mission. The Voyagers were preceded by Pioneers X and XI, while Mars was visited by Vikings I and II. Later either a backup was found to be unnecessary, or the money just wasn’t there.
In another amazing event this year, China just landed a probe on the moon. The Appolo moon landing marked the high water mark of US domination of the world. Good science is our best means to remain number one. Our soldiers can’t do that; our market position is vulnerable.
@Kathy:
Hunter-gatherer homo sapiens at various points have decided to do things like sail a canoe to Easter Island. You don’t stumble on Easter Island because you’re just looking for food.
@Michael Reynolds:
So how did they get to Europe? And the far reaches of Kazakhstan? (and probably further, an absence of evidence is not evidence of absence) I find it most likely that Neanderthals were wiped out by some bug brought up from Africa that Homo Sapiens were immune to, not because HS were innately more intelligent or that their curiosity gave them an evolutionary edge.
@Michael Reynolds: Shows what you know. You can’t make Snowman pancakes without the batter running together. Or teddy bear pancakes or Mickey Mouse pancakes, either.
@Guarneri: You’re mailing them in again. Sad. Low Energy. Pathetic. Also, I don’t recall “fake moon landing” as a leftist meme.
@Michael Reynolds:
Unfortunately hunter gatherers and early agriculturalists left no written records at all, seeing as they had no writing, and thus we’re left with inferences from archaeological evidence. Inferring actions is hard enough. Inferring motives is almost impossible.
For instance, a site in Turkey called Gobekli Tepe appears to be a temple, which was built in the stone age before agriculture or sedentarism became the norm for our ancestors. This suggests stone age hunter gatherers knew how to return to a place. Similar, though far less impressive, constructs reinforce this notion. But we don’t know how they knew where places were or how to get to them.
Exploration for its own sake is a recent development. No one is making huge fortunes off New Horizons (I think NASA makes the data available for free). People in the age of exploration did leave written records behind. We know the purpose of all those expensive voyages, and mostly they were to make money, or to find routes to markets where money could be made (BTW, how believable is it that a desire for flavorful meals resulted in the building of ships, the making of war, the decimation of native peoples, and the enslavement of millions of people?)
So as to the question, why did people sail in dugout canoes across vast stretches of the Pacific, we don’t have a definitive answer.
@Kathy:
As our ability to uncover the ancient past improves (and from my layman’s perspective, it has remarkably improved over the last decade), we are finding that the relationship between homo sapiens, neanderthals, and denisovans* was much more complicated than we originally thought. While there’s evidence that humans and neanderthals would sometimes fight, recent findings in Siberia, Iberia, and other places show evidence of extensive interbreeding. And we know some parts of the population have upwards of 3% neanderthal DNA.
*As evidence of our improving tools to uncover the past, we didn’t even know there were such a species as the Denisovans–let alone that they interbred with us–until about 5 years ago.
Moderators: please spring me from moderation. Not sure why spam filters caught me this time–I didn’t even have a link in my comment.
@Kathy:
Even more, they appear to have developed pretty advanced knowledge of astronomy.
(There’s a lot of crap out there about any ancient site and astronomy, especially when it comes to ancient people’s knowledge of equinox precession. In this case, I think the evidence is fairly strong.)
My understanding of the Gobeklie Tepe is that:
-We’ve barely begun to uncover the site.
-There’s an even larger site just a half kilometer or so away.
@Neil Hudelson: The number of very early buildings and megaliths that orient to the rising/setting points of the planets is amazing. It includes the Native American ‘mounds’ and Mesoamerican cities. These are also the points of reference for the Polynesian navigators who roamed the Pacific and found every significant piece of rock or coral there. That art is still taught and works well with modern maps/charts; not too long ago a circumnavigation using traditional (no compass, no charts) methods only was featured in the sailing/cruising media. Those ‘primitives’ also knew how to recognize and use currents and wind-patterns that didn’t intrude on modern knowledge until satellites were available to us.
I bet their catamarans didn’t have Lucas electrical systems.
@Neil Hudelson:
I often wonder why astronomy was so important to the ancients.
Sure, a good calendar is very helpful for farmers. It may even be of help to roaming bands of hunter gatherers (BTW, we need a shorter term for hunter gatherers; how about “foragers”?). But they went well beyond the calendar.
Odd tidbit. the calendar in use today is pretty much the one Julius Caesar commissioned in the first century BCE, known as the Julian calendar. It was reformed in 1582 by Pope Gregory XIII to better correct for the fact that the year lasts 365.2422 days rather than 365.25.
There’s a joke in historical/archaeological circles that when one is uncertain as to the purpose of an object, building, or action, it’s classified as being of “ritual significance.”
I wonder if that’s true of astronomy, past such practical applications as the calendar. Although to the ancients, the position of Mars in the Zodiac for astrological purposes might have been a practical application. We know they took ritual, and in particular religious ritual, extremely seriously.
yeah, that stuff been majorly revised over the last decade. We thought we had a fairly good grasp on the Neanderthals being dumb, etc but the real story is turning out to be much more complicated and nuanced, and we’re not close to done with figuring it out.
@Kathy: It costs a lot less to send a robot probe anywhere than it costs to send people.
If you want to send humans to Mars, the most practical solution is to send robots first; to assemble habitation and engineering modules, mine oxygen, and mine the fuel for the return trip. If humans already have all that safely in place, the payload, cost, and danger of the human voyage will be far less.
@OzarkHillbilly: It costs a lot less to send a robot probe anywhere than it costs to send people.
Perhaps. One theory is that Neanderthals were more specialized and intellectually less flexible.
Should be:
@OzarkHillbilly: I find it most likely that Neanderthals were wiped out by some bug brought up from Africa that Homo Sapiens were immune to, not because HS were innately more intelligent or that their curiosity gave them an evolutionary edge.
Perhaps. One theory is that Neanderthals were more specialized and intellectually less flexible.
@Zachriel:
Robots are not that reliable yet. and that’s too bad. But we could send habitat modules, food stores, water, and machinery to mine oxygen and make fuel ahead of time, over years, before sending people. Perhaps some automated machinery could work on its own for a while.
But the costs are still very high.
There’s also the matter of radiation. I’m not sure humans can survive long term exposure to it outside the Earth’s magnetic field. The Apollo astronauts took mere days for their trips. A Mars trip, two-way, would last several years. Some kind of shielding would be needed. In Mars, soil could work for shielding. In space, perhaps water tanks enveloping the inhabited portions of the ship (this is something Musk doesn’t talk enough about).
@Zachriel: Living in a nation with conservative/right wing parties, (i.e. most of the nations that can make the trip) who’s going to “come back” from Mars, anyway?
@Kathy:
This just begs for a citation to Motel of the Mysteries.
@DrDaveT:
Looks interesting.
I read a short story long ago along those lines, though the future archaeologists were aliens. Pay toilets were correctly identified as toilets, but they speculated the sacrifice of a metal disk was a requisite. They were certain that sections on trains labelled “smoking” referred to darker skinned humans, while “non-smoking” was a reference to whites. And they were puzzled as to why no human remains had wings, seeing as how much art portrayed winged humans.
More seriously, there’s a place in Europe where scientists have been recreating a medieval castle, not full scale, using known medieval techniques and materials. This is a common practice that allows one to understand the past a little bit better, though usually the scope is more limited. Now, suppose centuries hence archaeologist dig up a European town with a contemporaneous medieval castle that doesn’t seem to have been lived in. They’ll be quite confused.
How is it that they can get a clear signal from that far away, yet I get signal drops and disconnects from one room away?
@DrDaveT: I read it a long time ago. During the 2008 Democratic primaries I wrote a post in which I discussed the book in order to make the (semi-facetious) point that, given that most US presidents are distantly related to one another (including Obama, who was then just a candidate), if future archaeologists studied our society they might conclude we live in a monarchy.
http://kylopod.blogspot.com/2008/01/us-royal-family.html