CNN’s Alex Mooney consults his network’s “poll of polls” and finds that, although nearly 60 million Americans watched last Friday’s debate between John McCain and Barack Obama, the race remains unchanged.
The new polls are bad news for McCain, who with only five weeks until Election Day is quickly running out of opportunities to shake up the race for the White House.
In a new CNN poll of polls consisting of surveys conducted entirely after the first presidential debate, Obama holds a 5-point lead over McCain, 48-43 percent. That’s exactly where the race stood immediately before the two candidates kicked off the presidential debate season in Oxford, Mississippi, four days ago.
“The ruling on last Friday’s presidential debate is in, and it’s a split decision,” said CNN Senior Political Researcher Alan Silverleib. “The debate changed nothing. Obama’s supporters aren’t shifting to McCain, McCain’s supporters aren’t shifting to Obama, and undecided voters are still undecided.
This largely conforms to my expectations, as expressed in my post-debate instant analysis. Neither candidate committed any gaffes and there were no particularly memorable sound bytes, so it’s not surprising that there was little movement. At the same time, that’s good news for Obama: Not only did he stand toe-to-toe with Mr. Experience debating (ostensibly, anyway) foreign policy and come out even but he had the lead to begin with so didn’t lose it.
The RealClearPolitics poll average, though, gives a somewhat different result. The race is almost exactly where it was a month ago but Obama has risen and McCain has fallen in the last three weeks, a trend that continued after the debate.
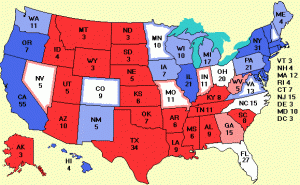More importantly, though, the much more important state-by-state polls are moving much more than the national polls. While RCP showed the race essentially tied for quite some time, Obama is suddenly breaking it wide open. Obama is up 249-163 (+86 votes) in RCP’s Electoral Count and, if leaning states are factored in, he’s got a whopping 348-190 (+158 votes) lead. Electoral-Vote.com shows an even larger 286-190 Obama lead, with 62 votes (Ohio, Florida, and North Carolina) too close to call.
I haven’t the slightest idea why the national race remains so close while the Electoral College race seems to be breaking so strong for Obama. Perhaps the financial crisis is felt more keenly in the swing states. Maybe the constant barrage of advertising is making a dent. Maybe Sarah Palin is less popular there. Honestly, I just don’t know. But it’s a worrisome trend for McCain.
We could, conceivably, have a race where Obama barely wins the national popular vote — indeed, falls short of a majority even without major third party candidates — yet wins by an Electoral College landslide.
