Teaching Math: Abstract Equations Beat Reality
Students learn math better if teachers stick to abstract equations rather than trying to bring in real world examples.
[M]any educators in recent years have incorporated more and more examples from the real world to teach abstract concepts. The idea is that making math more relevant makes it easier to learn. That idea may be wrong, if researchers at Ohio State University are correct. An experiment by the researchers suggests that it might be better to let the apples, oranges and locomotives stay in the real world and, in the classroom, to focus on abstract equations, in this case 40 (t + 1) = 400 – 50t, where t is the travel time in hours of the second train.
[…]
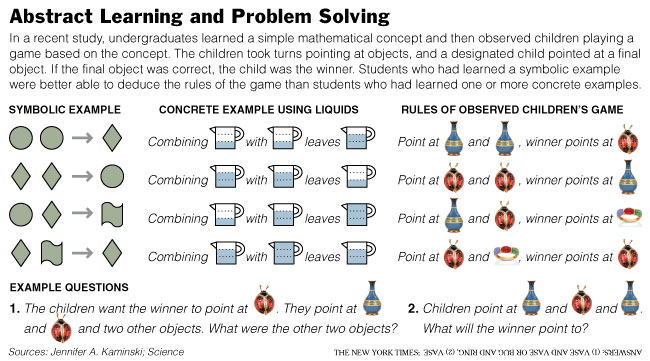
In the experiment, the college students learned a simple but unfamiliar mathematical system, essentially a set of rules. Some learned the system through purely abstract symbols, and others learned it through concrete examples like combining liquids in measuring cups and tennis balls in a container.
Then the students were tested on a different situation — what they were told was a children’s game — that used the same math. “We told students you can use the knowledge you just acquired to figure out these rules of the game,” Dr. Kaminski said.
The students who learned the math abstractly did well with figuring out the rules of the game. Those who had learned through examples using measuring cups or tennis balls performed little better than might be expected if they were simply guessing. Students who were presented the abstract symbols after the concrete examples did better than those who learned only through cups or balls, but not as well as those who learned only the abstract symbols.
The problem with the real-world examples, Dr. Kaminski said, was that they obscured the underlying math, and students were not able to transfer their knowledge to new problems. “They tend to remember the superficial, the two trains passing in the night,” Dr. Kaminski said. “It’s really a problem of our attention getting pulled to superficial information.”
Very interesting if incredibly counterintuitive. I was always reasonably good at math but it eventually reached the level, somewhere in second semester calculus, where it just became too abstract for me to grasp. It was just memorizing equations, which I could do, but it didn’t translate into actual learning in my case because I could no longer figure it out for myself, as I could with “real world” models. But, at least within the parameters of this experiment, this experience apparently isn’t the norm.





Very interesting indeed, but I suspect that those using the concrete examples did worse because the examples aren’t all that concrete: the water volumes are sometimes additive, sometime reflect a remainder, with no explanation of where the ‘rest’ went. Real world examples can be very useful math tools if they are in fact analogous to the abstract concept. Sometimes there is no real-world example for an abstract idea, where symbols function very well.
The problem many have with abstract math or anything outside of a basic or general system we typically use is their refusal to think outside the box. Just like in the experiment, if they are given something familiar they will become fixated on what is familiar. If you don’t allow them in the box then it easier for them to look for solutions outside the box. Of course giving them concrete examples helps. Like having a bowling ball and telling someone to draw a square on it. It helps to teach them Spherical geometry and that squares don’t have to have 90 degree angles just four equal angles. Explain this with words at a bar and you usually get nowhere with the consensus at the end by the patrons that all squares have four 90 degrees corners.
Also I agree as stated previously, not all abstract mathematics have solid real world examples.
Real world examples tend to work quite well when teaching children to add fractions (ex 1 & 3), but are much less effective when explaining multiplication of fractions (ex 2 & 4). It does not appear from the examples given that different connectors were used to differentiate when combinations were additive or multiplicative. It would be interesting to see if using connective symbology would alter the results.