The Hockey Stick and Global Warming
Not too long ago Steve McIntyre had an intereting post on some of the additional information that came out due to the Barton Hearings. One of the things of note is that Mann, Bradley & Hughes (MBH98) calculated the cross-validation statistics, but that these statistics were not reported. This is interesting in that it raises the question of why not report the results? One could surmise that the results were adverse to their position (which points towards dishonesty) or that such statistics are not necessary. The latter position though raises yet another question: why calculate the statistics. This isn’t a canned program that does the calculations automatically, these calculations had to be coded in. Further, McIntyre argues that the statistical significance of the 15th century reconstruction was lacking in statistical significance. So it seems the reasonable conlusion is that the statistics were insignificant since if it were otherwise why withold them from the article and referees?
Now some might be saying, “And what does this mean?” Statistical significance of a statistic indicates whether or not there might be a relationship there. For example, in introductory econometric text books one can often find an equation that relates consumption to income.1. The researcher wants to know whether or not there is a relationship between consumption and income. This is where statistical significance comes in. If the result (for the income coefficient) is not statistically significant then there is likely no relationship.2. Statistically significant results also is not proof of a relationship, but it does indicate that such a relationship is more likely.3 So statistical significance is a necessary condition for determning if there is indeed a valid relationship there or not. As such failing to meet this necessary condition is typically seen as a “bad thing” for your chances at publication.
Another interesting post is this one that deals with Preisendorfer’s rule N. Now, I don’t know much about Principle Component Analysis or Preisendorfer’s Rule N, but I do have a pretty decent grasp of mathmatics and statistics. From my reading of that post we see some interesting things:
- Preisendorfer̢۪s Rule N is a necessary condition, not a sufficient one: this means that passing this hurdle is good, but not good enough in terms of statistical validity. Think of it as a sporting event with preliminary heats where the winner of each prelim goes onto the final. Winning your prelim is necessary to winning the final, but not sufficient in that you could come in last in the final.
- According to Preisendorfer himself, passing this kind of test is and indicator to look deeper at the series and make sure that there really is something there.
- With regards to the Bristlecone Pine series while the series passes Preisendorfer’s Rule N, there is a problem in that CO2 fertilization could explain the robust growth. In other words, the Bristlecone Pines series isn’t a good temperature proxy.
- With regards to the gridcells used by MBH98 one gridcell has 16 cites, the others have 1 cite. This last one seems a bit esoteric, so think of it this way. Supposed we are interesting in a new teaching method in California schools. I sample 30 schools and at one I look at the performance of 25 students and at the other 29 I look at just one student. Basically, the one school with the large number of students is over-represented. This kind of thing is one problem Preisendorfer actually warns about.
What all this says to me is that the statistics in MBH98 has got some serious problems and Mann, Bradley and Hughes need to be more forthcoming.
Now, to head off the typical responses. First off I don’t work for the oil industry. Second, I agree that this is just one part of the argument in favor of the Global Warming/Climate Change issue. Even if it turns out that MBH98 is complete horse crap there is additional evidence that proponents of Global Warming/Climate Change can point too. The main point here is that this appears to be shody research. Further, this research is pointed to as part of the basis for enacting sweeping policies that could cost trillions of dollars. I don’t think it is too much to ask that these guys at least be more upfront and cut out the lame rhetoric about intimidation.
_____
1The equation might look like,
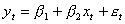
Where y is consumption, x is income, and the last term, ε is the error term.
2There are additional issues such as autocorrelation of the error term, multicollinearity between the explanatory variables, and so forth that can come into play here, but while these are valid concerns it is a bit beyond the scope of this post.
3The reason that it isn’t proof of a relationship is that there are also problems with spurious correlations, omitted variables bias, and specificiation issues. For example, a sine curve would over several complete cycles would show no trend. But if we started at the minimum of one cycle and then stopped at the maximum of another cycle we could end up with a statistically significant positive trend when in fact none really exists.