Chart Of the Day: How The Income Tax Grew
An interesting chart from Catherine Mulbrandon:
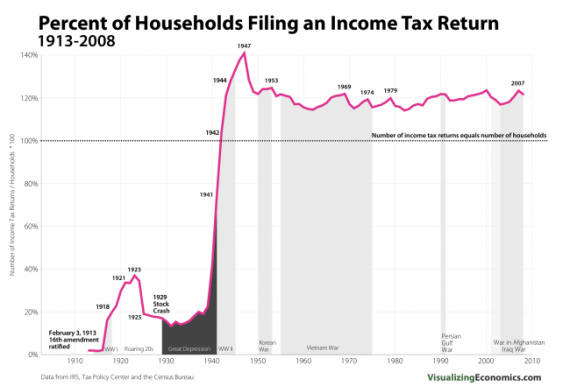
In 1913, 358,000 returns were filed which was 2% of all households. While the top tax rate was 7% on incomes above $500,000 ($10.9 million in 2010 dollars), the first $3,000 ($65,331 in 2010 dollars) was exempt from the the income tax for single persons.
(…)
In 1942, 36,619,000 returns were filed and the exemption had been dropped to $500 for single persons ($6,613 in 2010 dollars). For the first time the number of income tax returns filed exceeded the number of households.
H/T: Matthew Yglesias






What happened to my comment?
so, before income tax, what were the primary souces of revenue?
You’ve hit upon a pet topic of mine, Doug.
So often the tax debate presumes that the natural state of the world is that government is owed, and the debate is simply over rates and who pays. There is scant attention to political and organizational dynamics.
The income tax was sold originally as something to be born by a miniscule portion of the population, and at trivial rates. But then those political and organization dynamics took hold. Shorter: Pandora’s Box. And here we are. And then the most insideous invention of all time: witholding.
One of your sometimes colleagues – Bernard Finel – and I have gone round and round on this many times. His view: “we” demand goverment services, so shut up and pay. Me: who “we” Keemosabe?? As our illustrious President is oft quoted: “only 3% of the taxpayers will be affected by this” so its OK to tax away, baby. Beggar thy neighbor. Look at your graph. How’s that argument been working out?
Its Drew’s and Milton Friedman’s Law: if you increase taxes, more people will pay than advertised…………..and it will just get spent. And then they will come for more. Those pesky political and organizational realities at work…..
My comment, I think lost when the original post was updated/replaced, was to note that it’s conservatives now who ask “why doesn’t everyone pay income tax?”
How many times have that “half don’t pay” claim been trotted out?
Perhaps we shouldn’t discuss the income tax without discussing that big jump in filing in the early 1940s. It wasn’t due to a sudden war-related surge in patriotism (or, at least, not just due to such a surge). It was an enormous increase in compliance as a consequence of withholding. Prior to that income taxes were voluntary in the sense that they weren’t paid up front but were paid at the back end out of reported income.
What was used before? Prior to the income tax nearly all of the federal government’s revenues came from import duties and excise taxes. However, that didn’t produce enough revenue to fund anything other than a token standing army let alone the vast welfare state and civil bureaucracy we fund now.
So the lesson is that war is the health of the state
This story is miss leading. The number of people filing tax returns has nothing to do with people paying taxis.
http://money.cnn.com/2009/09/30/pf/taxes/who_pays_taxes/index.htm
The top 10% of the households only pay 70% of the income tax. Comrade Obama, the Great One, is correct as usual, we need to soak the rich even more to pay down the national debt and to help support those that pay no taxes,
http://www.ntu.org/tax-basics/who-pays-income-taxes.html
I wonder how that graph correlates to one that showed America’s percentage of world military spending? I suspect there would be a huge overlap.
Dave Schuler for President
Correct. Withholding acclimated people to the taxing concept. People gage to take home pay, or the monthly payment, not to the top line. “I make $70K/yr changed from ‘I make $70K/yr to ‘I make $50K net’ and that’s how I gage my expectations from my employer. They never think about total employment cost, or the government graft, er, take, er, tax.
But the jig is up. Confidence games have limited lives.
Apples to oranges. There is no relationship between the number of people filing tax return and government spending.
Excise taxes
Tariffs?
Wow, there are a lot of returns out there getting filed. Seems like it might be a good opportunity to start-up a business, like the type you find here.