Government Debt is Currently Cheaper Than Cash
Right now, it's more prudent for the Federal government to borrow money than to pay cash.
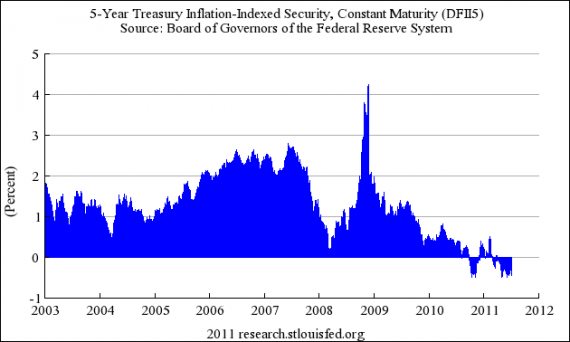
The graph above, which I snagged from Karl Smith, illustrates the point that concern for the deficit at this point in time is simply absurd. This is a graph of interest rates on Federal debt. You will note that at this time, interest on Federal debt is actually negative.
Let that sit in your mind for a minute. The interest rate is negative.
That means that right now, it is actually cheaper for the Federal government to borrow money than to spend cash. Which means that it makes more financial sense for the Federal government to borrow money than to spend cash. Which means that all the haranguing about the size of the deficit right now is pointless, because taxpayers are actually getting a better deal by having a deficit than if we had a balanced budget.
No, it won’t be like this forever. Yes, the deficit is a long term problem.
But it isn’t today’s problem. Not by a long shot.





Martin Wolf wrote a good FT piece on all this. Google “From Italy to the US, utopia vs reality” for access.
It’s sad.
Read “The Theory of Money and Credit,” by Ludwig von Mises. It was written about 100 years ago. It’s still apropos today. Leftists, unfortunately, never learned its lessons. Never were capable of learning its lessons. The world today suffers as a result. Soon things will get far worse too.
What’s sad is we should be using this opportunity to be investing in long-term infrastructure projects. They quite literally will never be cheaper. Instead we’re having a conversation about whether we should voluntarily create a sovereign debt crisis because Europe doesn’t have enough or something.
Yes Yes Yes Yes, a thousand times Yes.
We do not have a debt crisis – if we did these interest rates would be going in the other direction. It’s a long-term problem….which is suicidal to deal with in the short-term. Slashing spending right now kills jobs – at least a hundred thousand of jobs by conservative estimates.
We should be investing in infrastructure hand over fist. It is simply the smart thing to do on so many levels. Which I suppose is why Washington, and silly people with tea bags dangling from their hats, don’t get it.
We will never ever build things as cheaply as we can now. Money is cheap. The construction industry is extremely competitive – in my office we are routinely seeing bids 20% below what we consider the real value of the projects. And there is a ton of labor out there – which we should be doing everything we can to put to work.
I’m not talking about welfare, or tax cuts. I’m talking about investment. Roads, bridges, airports, high-speed rail, the energy grid. Whatever we can think of.
Tsar buddy, Mises may have been right in general without being right today.
There are general circumstances, and specific circumstances.
I will put a bit of light between my position and Norm’s however.
We do have a deficit and debt problem. Definitely. At the trivial level, it’s because this deficit and debt were not well-designed, and not intended to solve the problems Norm and the llama would have us address.
At a second level though, it is a crisis if it is a long term crisis.
To say it is not a short term crisis might be defensible, but not to say it is no crisis.
So what we should do is borrow 14 trillion to pay off all of our debt which would eliminate interest payments, right?
Hate to point this out to those pushing for more “free” borrowing, but that negative interest rate is on short-term borrowing. If we could borrow the money and pay it off within 5-10 years then that would indeed be a good deal. What are the chances of that happening?
And keep in mind we are already borrowing over a trillion dollars a year….
Now we’re dealing with semantics…a crisis is a turning point…a moment that requires decisive action. That is not what we face now – except for that doing something stupid like slashing spending may make it so prematurely. It’s a problem. We have lots of them.
I am not saying we should just mindlessly spend dump-trucks of money like Bush did. I am saying that we can make smart investments today that will help our very real immediate crisis – lack of demand and hence unemployment – which in turn will help the long term problem of the debt.
Look at the out years (figure #1 at the link below). The economic downturn is a big factor in the debt. Making the right moves now helps us down the road. Slashing spending now, and in turn jobs, weakens demand even further and makes the problem worse not better.
Yes, the debt is a long term problem. Which is why it makes sense to deal with it now, when interest rates are low, than at some point down the road when T-Bill rates have risen to the point where interest on the National Debt eats up an unmanageably large of the budget.
Sure, Doug. I’m down with a “Grand Bargain” of sorts (though my preferred ratio of spending cuts to tax increases is somewhere between 2 to 1 and 3 to 1), and so are plenty of other Democrats. The long-term problem should be headed off at the pass.
Doing it this way, as part of the debt ceiling vote, is ridiculous, but that’s the GOP for you.
A deal that phases in spending cuts and revenue increases over time is the way to go. You slow down the runaway train. You do not slam it into a brick wall and say “excellent, we’ve stopped the train!”
You know this. Your party apparently does not.
If the world were going to end in a week, you’d be absolutely right Alex. However, interest rates won’t always be low and we still won’t have paid back whatever we borrow now so we’ll be paying interest on that, too, and at a higher rate.
@Rob in CT:
I don’t belong to any party and I’ve made my views on the debt ceiling negotiations well known in several posts this week.
Tsar’s comment reminds why modern conservatives have begun to mimic late-stage Marxists;
Every practical problem becomes for them an exercise in Grand Dogma, solvable by simply reading a century old manifesto.
Should our nation inflate demand thru government infrastructure construction, or halt spending so as to erase deficits?
Read the Holy Writ, and all will become clear.
This is religious fanaticism, not governance.
Sort of reminds me of “deficits don’t matter” and “stay the course.”
As Dr. Schuler says, interest rates will be low right up until the point they aren’t. And then you’re left with an even worse problem. Like I posed elsewhere a few days ago it is like a guy way, way over his head who thinks that as long as he can keep paying the monthly minimums on his credit cards there no real problem. After all, there’s always those guys on the radio who offer to negotiate your debt down for you. Wonder why the PIIGS haven’t taken advantage of their services yet.
I think the problem with this chain of thought is that interest rates are low because the Federal Reserve is buying up treasury bills in order to keep the interest rates low. How long can that continue?
Speaking of absurd positions…..the debt issue is not real??
Several commenters have pointed out that this is a long term issue. It has also been pointed out that rates may rise after the end of QE.
May I just add, dear fellow commenters, that there are two components to debt service – interest and principal. Just because interest has been intentionally engineered to unsustainable lows doen’t mean that the principal has disappeared.
Endeth the Credit 101 lesson.
C’mon, Alex. Really?
@Doug Mataconis: Our infrastructure deficit is a long-term problem. Our unemployment crisis is a short-term problem, one that also exacerbates our deficit problems. If we are going to spend money on repairing and updating our infrastructure – which, along with being necessary, will also put people back to work – we will be better off than if we decide that dealing with our debt is the most important short-term action. The best way to reduce the deficit is by putting people back to work.
Let me add a couple of other factors that haven’t been mentioned. First, we know that, barring some major reform that we have so far refused to make, we are entering a period during which we’ll see a sizeable expansion of government spending over a protracted period due to the retirement of the Baby Boomers. This is not a surprise. We’ve known about it for sixty or so years.
Second, there’s very little reason to believe that our growth rate for the foreseeable future will be high enough to pay those additional expenses from revenues, at least not without substantial increases in those revenues by increasing their marginal or effective rates. That’s being resisted.
Is this really a good time to undertake addtional debt?
The government is not “… a guy way, way over his head…” in credit card debt. As long as people don’t understand that the government is not an individual, and it’s not a business, and it doesn’t operate in the same ways, they are going to continue to not understand the situation. Clearly.
“The government is not “… a guy way, way over his head…” in credit card debt. As long as people don’t understand that the government is not an individual, and it’s not a business, and it doesn’t operate in the same ways, they are going to continue to not understand the situation. Clearly.”
Pure crap. Or as the French might say – “gar-bahjjzz” Governments have the same concept as individuals or corporations: terminal debt capacity.
Drew, hmm…, so is the US facing Chapter 7 or Chapter 13 bankruptcy?
There are, of course, differences between persons, corproations and governments, but there are also similarities and it would be nice to see our freinds from the Left at least acknowledge that there are in fact some basic rules that still apply when it comes to fiscal matters for governments.
I’m a moderate – not from the left – but I will acknowledge a couple basic rules:
– slashing a hundred thousand + jobs when it is not necessary is just stupid.
– risking an economic catastrophe for purely ideological reasons is just stupid.
– confusing a crisis of demand with a debt crisis is just stupid.
– walking away from the biggest deficit reduction deal in history because grover norquist demands it is just stupid.
It’s negative, but only ony the inflation protected securities. That should be a big red flag that people think the inflation rate is going to go up shortly.
hey norm is a moderate. Just ask him.
@Dave Schuler: “Second, there’s very little reason to believe that our growth rate for the foreseeable future will be high enough to pay those additional expenses from revenues, at least not without substantial increases in those revenues by increasing their marginal or effective rates. That’s being resisted.”
Bingo – In fact since we are near the end of cheap resources, not just oil but nearly all non renewable s, we will never again experience the growth we have had in the past. Our current economic system which depends on credit can’t be sustained without growth. This applies not just to the US but the world and not just to government but business too.
@Tsar Nicholas II:
Dont worry Tsar, you’re the only one so far who knows what they’re talking about 😉
I’d take a different tack than others on why the long term debt problem needs to be addressed soon:
While we’re talking, the problem is multiplying.
This isn’t a static problem, like a bed that needs to be made, and can be done later. The bed grows.
Well, I am going to be living in a ghost town pretty soon as we also have a job problem. And you will not have economic growth as we knew it. The demand has to come from the government as the private sector is failing us.
More bad news for my town.
http://www.thecourier.com/Issues/2011/Jul/14/ar_news_071411_story1.asp?d=071411_story1,2011,Jul,14&c=n
@Drew: glad to hear that, drew. so i CAN print some money to cover my credit card debt, cause i am not different from the gubmint.
may as well use my eminent domain powers to stop paying my mortgage, by the way…