55% Of Republicans Believe Obama Was Born In A Foreign Country?
Kevin Drum and Daniel Drezner both write today about a poll conducted by Dartmouth Professor Benjamin Valentino [PDF]. Principally, the poll seeks to measure public opinion on a wide-ranging variety of foreign policy issues but sprinkled among the 65 questions are several domestic policy questions and, well, this:
Half of Republicans believe Obama was born in a foreign country? Still, even after all the evidence that has come out? I’ve never been one to underestimate the resilience of the birther movement, but they’ve always been a fringe movement and that number seems exceedingly high to me. If it is true, then the GOP has a bigger problem than I ever thought.

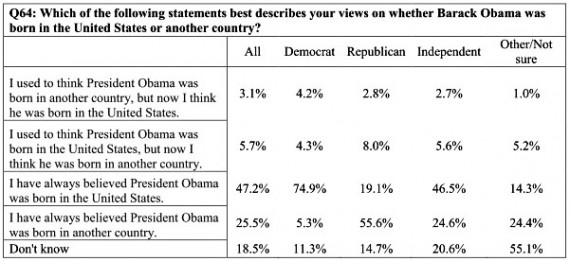






That sounds high. I thought it was pretty stable at around 40%. And of course there is the neverending debate over whether they “really mean it” or if it’s just a tribal shibboleth.
I suspect shoddy polling methodology, given this seems an outlier from previous such polls.
Anyway, the crazy is apparent in GOP policy proposals. I don’t need birtherism to illustrate the crazy for me.
Is there some equivalent to Rome and their lead pipes?
Seriously, is this normal human irrationality, or are we worsening?
@Rob in CT: The closer we get to the election, and the more apparent it becomes that Obama is going to win, the higher the number is going to go.
I think this result is skewed by the percentage of Americans who don’t remember that Hawaii is actually a state.
How are you defining “fringe”?
Most people would define it something like “Something believed by a few % of a group, and espoused by virtually no one in official power in the group”.
What % of Republicans are you claiming are birthers, based on what evidence? Because if that 40% stat is accurate, doesn’t that make it rather disingenuous to call it “fringe”?
Actually, this poll says it’s over 63%, as you need to add in the 8% of Republicans who originally believe he was born here and switched to believing he was born in another country.
Fringe? Romney has embraced Trump, and Trump is birtherism with a capital “B”. This is mainstream GOP thought.
@swbarnes2: Indeed. If this poll is truly representative, it’s no longer unreasonable to simply label the “typical Republican voter” as a gullible, thick-headed moron.
I weep for our nation.
The independents don’t come off too well either.
I don’t know why people are continually surprised by things like this.
1) The GOP is fused with Fox News and Rush Limbaugh — bold and shameless liars who profit by feeding GOP rage and resentment caused by a loss of status by older, less-educated whites..
2) Politics is emotion, and the GOP’s emotions center on rage and a sense of victimization. The persistence of birther beliefs is a product of those emotions. It is racism barely concealed by a thin veneer, and as usual racism is the product of fear and ignorance, both hallmarks of modern Republicanism.
I don’t know how this could be any clearer or any more easily explained. The GOP is the old, stupid, white folks party. Old, stupid white folks feel themselves isolated and falling behing. They need a myth to explain their loss of status. The myth in question is one of victimization. These folks see themselves as victims of immigrants, blacks, the young, gays, unions, the well-educated, etc, all of which support Mr. Obama.
They can’t give up on the myth. Without the myth they have nothing. The intellectual underpinnings of Republicanism are simple nonsense, so made up victim narratives are all they have left.
@john personna:
It’s supply and demands: the cost of irrational behavior has dropped, so like any economic good, this has caused the demand for it to increase.
Doug closes by noting about this poll result that, “If it is true, then the GOP has a bigger problem than I ever thought.” I just finished reading Chris Mooney’s The Republican Brain: The Science of Why They Deny Science – and Reality. Doug, the GOP has a bigger problem than you ever thought.
Highly recommend the book, very good, except for an absence of much advice on any feasible response. I thought it might be helpful in terms of how to get my conservative friends to accept just a few, basic, demonstrable facts. The answer seems to be, you can’t. A strong argument just produces stronger denial. And smart, educated conservatives are worse, they just build more elaborate defenses.
53.3% of Republicans refuses to do anything to cut the deficit.
64.5% of Republicans think it’s very likely that Iran will nuke Israel.
62.9% of Republicans think Iraq had weapons of mass destruction in 2003.
It’s clear from this poll that Republicans live in their own little world…
@Rob in CT:
This speaks to one of the greatest problems with quantitative polling — you have to assume that people are transparently responding. For once, I would like to see some polling group do actual qualitative followup with these folks to understand whether or not they are just screwing the pollsters (after getting pissed off that they are even being asked the question).
One of the things that ethnographers know is that screwing with the researcher is a time honored tradition… I have to think some of these responses were just that.
It would also be helpful to try and dig into the demographics of those who responded in that way.
I read the headline. But I stopped reading the post after “poll conducted by Dartmouth Professor”.
The poll was conducted by a respecting national polling firm with the professor being the one who gathered the questions and helped interpret the data
@Rob in CT:
I agree. Case in point, I notice that they don’t include “I don’t really give a d&^%!”
Also, note the independent stats. Rough calculations (too lazy to add right now) says north of 40% do or did believe that Obama was born in another country (include the 20% that “don’t know”?). Can’t say I buy that.
The Republicans you talked politics with over pizzas and beer in the college dorms are not the same people who inhabit today’s Republican Party. The GOP gets a presumption of good faith that is entirely unwarranted by their current actions. This crop of Republicans are nihilists and liars.
I want the GOP to be patriots, to believe in their issues passionately and to conduct themselves with the honor, intellectual rigor and dignity that the term conservative implies. I won’t agree with them, but I will respect them. This group does not pass the test. Until right-leaning independents and moderate Republicans remove the nihilists and charlatans in the GOP drivers’ seat, there really is no hope for the GOP or the USA. Please stop enabling them with the false equivalencies between the parties. They really are that far gone.
Until the GOP suffers for propping up the fools and grifters (such as Limbaugh and Fox News), they will continue in their ways.
@Doug Mataconis: Correct, but that doesn’t negate my point about the limits of quantitative methods on that sort of complex question.
@legion:
I believe Legion is onto something here. I wonder how many Americans do believe that Hawaii is “foreign” or at best occupies a status similar to Puerto Rico? That would be an interesting follow-up question: “Is Hawaii an American state?”
doug:
Doug, are you suffering from severe amnesia, or is there more than one Doug Mataconis who posts here? Because someone using that name wrote this last year:
47% doesn’t fit any definition of “fringe movement,” so your statement (“they’ve always been a fringe movement”) is quite mysterious. Also notice that “all the evidence that has come out” came out prior to that poll you cited last year. So there’s no news here. This latest result is not far from the earlier result, so this poll is not too interesting. What’s interesting is how motivated you are to deny the reality that your party has been taken over by nuts.
anjin-san:
Exactly. Trump embraces birtherism wholeheartedly, and Romney embraces Trump wholeheartedly. It’s natural that this choice by Romney would have the effect of convincing more people to embrace birtherism.
By the way, this is the NYT statement you cited last year:
What’s interesting is that NYT has scrubbed that statement from the article. MM noticed. They point out that the poll is referenced in a different NYT article. Also, it’s referenced here.
I absuty believe the results of that poll.
It is consistent with my feeling that base Republican and movement conservatives have not accepted as legitimate the last 2 elected Democratic presidents. The GOP has successfully created an alternative reality with their own media to reinforce the message that Democratc presidents are not legitimate.
@Tsar Nicholas:
Dartmouth is well known as the most conservative Ivy League college.
So others might see this as indicative of a possible conservative bias. I don’t, I think a majority of GOP voters support the Birthers in the effort to call into question Obama’s legitimacy.
@michael reynolds: It’s easier to blame others for your own failures. I used to when I was younger, and I also used to be a Republican. Funny, when I started taking responsibility for myself I became successful and a Democrat (and much happier, not coincidentally).
@al-Ameda:
To be fair, a significant amount of base Democrats and movement liberals didn’t accept either of GWB’s elections as legitimate.
And I know that this will probably get at least one response of “but 2000 clearly wasn’t” which in part proves this point. It also demonstrates how Bush v. Gore, as an intervention, has helped damage the overall legitimacy of the Presidency.
The question will be when will this trend of seeing the president as “illegitimate” end (to be fair we should remember that a lot of Democrats at the time believed that secret deals with Iran over the hostages gave Reagan his first win). Likewise Republicans blamed Kennedy’s defeat of Nixon on the dead voting… so perhaps this is a far older trend then we lead ourselves to believe.
@mattb:
Republicans investigated Clinton for 6 years and impeached him.
Democrats, to my knowledge, never contemplated a retaliatory impeachment of Bush.
Bottomline – Republicans have the fire and the commitment, Democrats do not.
mattb,
“To be fair, a significant amount of base Democrats and movement liberals didn’t accept either of GWB’s elections as legitimate.”
I know lots of people who think 2000 was illegitimate. 2004 is held illegitimate only by fringe loonies. Far more Republicans felt both Clinton and Obama’s elections were illegitimate, even though they were elected by far wider margins.
@al-Ameda:
Alternatively, in this case at least, the Democrats rose above copying the Republicans in wasting tax payer money on pointless political attacks?
The Republicans seem to regularly forget that they claim to be against gov’t waste.
55% of Republicans are ignorant morons? I would have taken the over on that one but it seems plausible to me.
Sadly, I suspect that 55% of Republicans don’t realize Hawaii is a state within the United States.
@george:
I suspect that 55% of the American people could not locate North America on a labeled map of the continents.
I suspect that 55% of the American people don’t know what a Honey Badger is…
http://news.yahoo.com/blogs/ticket/scott-walker-gets-honey-badger-d-180452742.html
@mattb:
Fair enough, but the “both sides do it” doesn’t go far enough because the parties’ responses and actions on this have not been anywhere nearly equal.
Republicans did not accept Clinton as legitimate and impeached him, and they do accept Obama as legitimate and 55% of Republicans do not believe he was born in America. Democrats’ disdain of the legitimacy of Bush is nowhere near the intensity of that of Republicans. Democrats went nowhere with it – nowhere.
@michael reynolds:
I remember vividly the wild conspiracy stories about Bill Clinton back in the day when the internet wasn’t necessarily used as a breeding ground for insanity. Imagine the type of stories we’d be hearing about Bill Clinton if the internet was as `vibrant` back then as it is today… I think what we’re seeing is the first Democrat president in this age of information. Rumors are much easier to spread and take root. Polls tend to show Republicans buy into these things a bit easier than Democrats, and polls also point to Republicans today being generally older and white (but certainly not exclusively). Because Obama is black, it’s very easy to attribute it all to `racism`, but in my opinion that’s all it is… easy. Really these things are going to be said about any democrat who is president. Obama had an opening with his family’s makeup, and they pounced… that’s all.
doug:
A similar example of how big the GOP’s problem is:
Also this: