77% Oklahoma High School Students Can’t Name 1st President?
 A recent survey of Oklahoma public high school students found that the overwhelming majority can’t answer even simple questions about U.S. government and history.
A recent survey of Oklahoma public high school students found that the overwhelming majority can’t answer even simple questions about U.S. government and history.
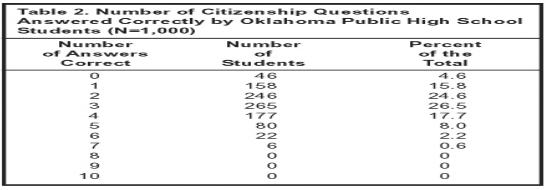
A thousand students were given 10 questions drawn from the U.S. Citizenship and Immigration Services item bank. Candidates for U.S. citizenship must answer six questions correctly in order to become citizens. About 92 percent of the people who take the citizenship test pass on their first try, according to immigration service data. However, Oklahoma students did not fare as well. Only about 3 percent of the students surveyed would have passed the citizenship test.
Below are the questions and results:
Question % of Students
Who Answered CorrectlyWhat is the supreme law of the land?
28 What do we call the first ten amendments to the Constitution?
26 What are the two parts of the U.S. Congress?
27 How many justices are there on the Supreme Court?
10 Who wrote the Declaration of Independence?
14 What ocean is on the east coast of the United States?
61 What are the two major political parties in the United States?
43 We elect a U.S. senator for how many years?
11 Who was the first President of the United States?
23 Who is in charge of the executive branch?
29
Shocking, no?
This meme is spreading through the blogosphere with the consensus being that our education system is failing and our students are dumber than a bag of hammers.
But here’s the thing: I simply don’t believe these results are accurate. I taught Politics 101 to college freshmen for a decade, so I’m under no illusion that our kids have a strong working knowledge of how our system works. (Indeed, having administered basic geography tests as part of my World Politics course, I’m shocked that 61% not only know the Atlantic Ocean but that they know east from west.) I could see students not knowing the answers to several of the questions above, especially framed as they are. But, seriously, your average 6-year-old knows who George Washington is. They couldn’t tell you anything about his administration, of course, but they know: wooden teeth, chopped down cherry tree, couldn’t tell a lie, Martha, and 1st president. It’s, frankly, trivia. (And hagiography in the case of the cherry tree fable.) But they know it nonetheless.
Tom Maguire took the time to click the link to the actual survey results. He observes, “in defense of the Oklahomans, a ten question test was administered by telephone to one thousand high school students. That has to be an unfamiliar format for the respondents, and probably not all of them gave it their best shot. Still, this is pretty grim.”
Actually, it’s worse than that. The exam was commissioned by a conservative activist organization whose mission is to show how lousy public schools are so as to advocate for home schooling and private, religious schools. Read the long diatribe that serves as the press release for the survey’s results.
Here’s how they describe the methodology:
In Oklahoma, the telephone surveyors called a sample of 1,000 public high-school students and read the following statement: “On the next 10 questions, I will be asking you questions about American government and history. Give me your best answer, and it is permissible to respond ‘I don’t know.'”
Guess what the most popular answer was on just about every question was. Yes sir: “I don’t know.” It was the majority response on the two parts of the Congress (58%) and who’s in charge of the executive branch (51%) question and was in the 40’s on three others. It was the number one answer on eight of ten questions.
How many of those were actually non-responses? Given the purpose of the exam, I wouldn’t be at all shocked if the survey firm wasn’t instructed to code non-responses as “I don’t know” rather than going on to a student who would take the time to give thoughtful responses. (The only thing holding back my confidence in this regard is that the Atlantic Ocean question is listed 6th and got a very high right answer rate.)
Interestingly, too, the right answer was the plurality actual response answer on almost every question. And the runner-up answers were, for the most part, non-idiotic. So, 17% thought the Declaration of Independence was the supreme law of the land, compared to 28% correctly identifying the Constitution and 41% “I don’t know.” Abraham Lincoln, Thomas Jefferson, Franklin Roosevelt, and John Adams were the most popular wrong answers on 1st president.
The chief “wrong” answer on the “Who is in Charge of the Executive Branch” question was “the Governor,” which garnered 10%. That’s actually right, since the question doesn’t specify federal or state. Similarly, shouldn’t the 11% who answered that the two parties are Communist and Republican be scored correctly? (I jest, of course.)
Again, I’m not Pollyannish on how much our kids know. In 2001, Steven Taylor had a bonus question on a multiple-choice test he administered to 101 students at the university where we both taught at the time asking who the vice president was. A woefully small number got it right. (In fairness, Dick Cheney was new in office and much less controversial than he’d be later. Also, Steve’s eldest son, then perhaps 6, knew the answer.) But a telephone survey of 17-year-olds who have no incentive whatsoever to take it seriously administered by a group that wants to prove how lousy our schools are is simply unfair.
UPDATE: Kevin Drum emails to point out something I totally missed: “not one single student got even 8 answers right.”
Kevin says, “That’s just not credible.”
No, it isn’t. Indeed, few people got more than 4 right! My strong guess is that: 1) they rotated the questions, rather than asking them in the order above and 2) the vast majority of students hung up after no more than three or four questions.




I like the idea that if you cold-call kids and ask them a series of political science/history questions — with a single geography question thrown in — you’ll get a representative sample of what those people know.
For most people, there are three thought processes to a survey like this:
(1) “This is inane, so I’m going to answer the questions as quickly as possible.”
(2) “Are these trick questions?”
(3) “I’m supposed to hang out with my friends. Better just say, ‘I don’t know’ to everything and get this person off the phone.”
I wager good money that about 3 people paid close attention to the questions and cared if they got them right or wrong.
This isn’t a new complaint. I remember a book that made the best seller lists about 50 years ago, What Ivan Knows That Johnny Doesn’t that lodged a similar complaint albeit with a focus on the sciences.
There are lots of reasons for it. Lack of value for education. Americans have a romantic streak: you wouldn’t want to spoil the pristine ignorance of innocent children with ugly learning, would you?
Part of the blame surely lies on the relevancy craze that hit about 40 years ago in which students got to decide what they should or should not learn. Unless you’re looking for a job as a docent or history teacher will knowing who wrote the Declaration of Independence land you a job?
And surely today’s inclination of too many parents to view the schools as adversaries rather than allies has something to do with it. Sure the schools should take some of the blame. Over the years they’ve transmogrified from places in which we make Americans (read John Dewey) to places where we can employ a lot of adults.
bzzzt…wrong answer.
The correct answer: They’re idiots.
That’s helpful. At least define “idiot” if you’re going to make the claim.
From Oklahoma, by chance?
I remember an East Side Kids movie I saw once (look ’em up, children). This old guy who was an immigrant from some place in Eastern Europe was preparing to take his citizenship test. He asked the kids a bunch of pretty basic questions about the Bill of Rights. None of them could answer the questions. Seeing the look of chagrin on their faces, he said something like, “Ah, don’t worry. You know the answers to those questions in your heart, in your blood, even if you can’t answer them with your mouths.”
This is like the “How was our service?” calls I get sometimes. My answers follow the same pattern:
1) Fine
2) Okay, great, whatever.
3) Yeah, yeah, you’re God’s gift to the stereo-buying public.
4) Are we done?
5) That’s it: F— off.
Click.
To be fair, some of the answers have changed in recent years. While I know the traditional answer to question 3, my first thought upon reading it today was “Dumb and Dumber.”
They might have got a higher correct response rate if they’d surveyed 5th graders.
I think James is taking all the fun out of this. Can’t we Northern elites just point our fingers and make mocking “hyuk hyuk” sounds?
/that is, until they test one of the Northern states as well …
“But a telephone survey of 17-year-olds who have no incentive whatsoever to take it seriously administered by a group that wants to prove how lousy our schools are is simply unfair.”
A bit off topic, but so is a fake “interview” at a community help organization requested by a “pimp and a prostitute” who are actually “journalists” entrapping the organization into discrediting itself.
How so? First, they didn’t “entrap” anybody. They went undercover in false identities to test out a theory. Journalistic outfits do that all the time as a legitimate way of investigation.
Second, this is how a goodly number of ACORN representatives acted. Is it a representative and comprehensive sampling? No. But it says something interesting about the group’s organizational culture. Not necessarily about the upper management — or, at least, not that they’re corrupt and like to help criminals — but something about the quality and type of people they employ.
Two points:
First, Mr. Joyner’s Politics 101 students really cannot be compared to random 17 year olds — the Politics 101 students have decided to go to college, and take Politics 101.
Second, this was Oklahoma. What do you expect?
Ok, the second point was more of a mean-spirited slur against the middle of the country, but the first point still stands.
I would still suspect that this survey was grossly flawed, but I don’t think we can use a comparison with more motivated college students to show this.
Classy.
Just can’t imagine how kids would not know how our government works…
Just can’t imagine how kids would not know how our government works…
Enlighten us with your wisdom, anjin-san, what does a Vice-President do, and be sure to target your answer to an elementary school audience.
Humor us.
Hey, anjin-san, maybe if win the bidding, (currently at $63,500) Governor Palin can have you over for dinner and explain the nuances of the Vice-Presidency to you. Go for it, you said you were rich, right?
Peter:
I thought you were the one who was rich. And with a very young wife, too.
Is Sarah entertaining bids for a night of “naughty librarian and bad boy author?” Because I’ll totally bring the thigh-high boots.
Interested:
By the way, have you had a chance to read Peter Brimelow’s book, “Alien Nation?” There’s a rave review at the National Vanguard (white supremacist web site.) I’ll just pull one fun graf:
Yes, one does wonder that about Mr. Brimelow, doesn’t one?
No, Michael Richards, I’m pretty sure it was anjin-san who exclaimed that he was rich. Now that you’re no longer on Seinfeld perhaps you could place a bid too.
Interested:
Oh, my God, he not only has German racial attitudes, the poor man, he’s stuck with their sense of humor, too.
Sorry, that was for anjin-san. Damned immigrants screwed up my typing.
Will she also tell him what the Bush Doctrine was and name the newspapers she supposedly reads? Just curious…
Will she also tell him what the Bush Doctrine was and name the newspapers she supposedly reads? Just curious…
She doesn’t need to explain the Bush Doctrine after she’s implemented it so successfully in regards to her preemptive kneecapping of ObamaCare. As for the newspapers, she can offer up the ones which publish her editorials and the ones which will report on her Hong Kong speech next Wednesday ( you knew there had to be a reason that President Obama signed on to open the UN session on that same day and to preside over the Security Council the next day – he wanted to steal her spotlight.)
Good all around.
Fanboy strikes again…do you seriously believe that Sarah Palin somehow “kneecapped” the president’s health care reform plans? Well, other than spreading lies about “death panels”…oh wait…I guess she did play a role…funny thing about those newspapers that will report on her Hong Kong speech…none of them will even be allowed in the room…let me guess, that’s because the media is an evil, liberal conspiracy, right? It has nothing to do with the fact that she might spout some inane nonsense like she did to Charles Gibson and Katie Couric…as for your delusions that the president is somehow basing his schedule on whatever will preempt her…that leads to a point that we can definitely agree on…that is, that we both would love to see her run against him in 2012…although I suspect that realistic conservatives like this blog’s host wouldn’t care for that scenario…
funny thing about those newspapers that will report on her Hong Kong speech…none of them will even be allowed in the room
So? The non-American press will seek out attendees and report on their impressions and the American press will follow standard procedures and make stuff up. Either way, there will be plenty of column inches resulting.
ah, thanks for providing some critical analysis, and thereby some hope that we are slightly less incredibly stupid than the survey suggests. But if you live in the U.S., are in High School, and you can’t name the 1st president immediately, you should be deported.
To be blunt, why should we care even if this survey was legitimate and the students didn’t know this knowledge? When I was in high school, I would have missed 1/2 these questions, but I knew far more math, physics, and chemistry than the average student. At that point in my life, that’s what was relevant to me. Who is the great arbiter that decides what knowledge is the fundamental knowledge that all citizens should know? As Dr. Joyner pointed out…trivia.
I went on to get a chemistry degree in college, and guess what? When politics became more important in my life, I learned what I needed to know to make myself a more informed voter.
Really, does anybody think that this is an issue? If so, I would legitimately be interested in hearing your arguments.
This survey was obviously completely fabricated–you can tell by looking at the alleged answers given to open-ended questions. For instance, 20 students (2%) answered the Monroe Doctrine was the supreme law of the land, but zero answered “Bible” or “Ten Commandments”? To the questions about the major parties, all the students either answered correctly, answered “Don’t know”, or answered “Republicans and Communists”. No one answered “Republicans and Socialists”, “Liberals and Conservatives”, or “Dickweeds and Douchebags”? Sorry, it’s just impossible that this survey was even administered, considering these results.