Kevin Drum catalogs some of the things that have happened to Rick Perry since he announced his candidacy on August 13th:
- Suggested that maybe Ben Bernanke should be lynched.
- Declined to back off his contention that Social Security is an unconstitutional Ponzi scheme.
- Called climate change a “contrived phony mess” that was cooked up by scientists who have “manipulated data so that they will have dollars rolling in to their projects.”
- Pissed off the conservative base by defending his decision to (in Michele Bachmann’s immortal words) give “government injections” to “innocent little 12-year-old girls.” Said Perry condescendingly: “What I don’t get is what parents don’t understand about an opt out.”
- Further pissed off the conservative base by suggesting that if you disagree with his policy on in-state tuition for illegal immigrants, “I don’t think you have a heart.”
- Mangled a prepackaged debate attack on Mitt Romney so badly, and then followed up with a statement on Pakistan so inscrutable, that even his supporters started to wonder if he has a three-digit IQ.
- Proposed that U.S. troops should be used to fight Mexican drug lords. In Mexico.
- Had to defend himself against revelations that his family leases a hunting spot called “Niggerhead.”
Now, it’s arguably true that some of these mis-steps have hurt Perry less than others. It’s unclear, for example, that Republican primary voters are really punishing Perry for his stance on climate chance. However, I don’t think there’s any question that things like his position on Social Security, the way he tried to defend his actions as Texas Governor regarding Gardisil and in-state tuition for children of illegal immigrants, and his bad debate performances have caused him to fall from grace in the eyes of many in the GOP. It’s unclear what impact the last two items might have simply because they just became public this past weekend, but it’s pretty clear that they’re probably not going to help.
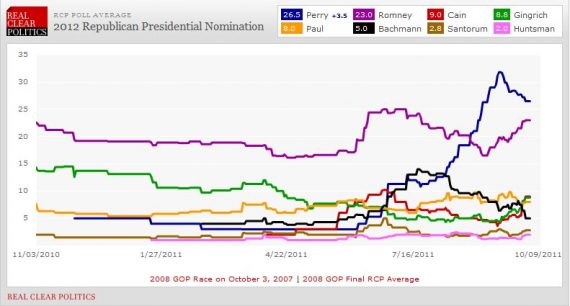
The impact on Perry in the polls has been substantial. Inside of about two weeks, he went from instant front-runner to falling star:
The most recent national poll had Mitt Romney in the lead, Perry second, and Herman Cain a surprising third. Perry is also showing weakness in statewide polling in important early primary states like Iowa and Florida. If that’s replicated in other polling likely to be released over the coming week or so, then Perry will have paid a steep price for so many fumbles in such a short period of time.
As I noted last week, Rick Perry is hardly out of the picture here. He’s still got a lot of appeal for the GOP’s conservative base, and he still seems to be more viable than any of the other Tea Party candidates in the race. Whether these hunting lodge revelations have an impact on that perception among Republicans is something only time is going to tell, but unless that happens he is still going to be one of the two top contenders in the race for the GOP nomination as we head into the final three months before voting begins. Of course, he’s going to have to address some of the mistakes he’s made already, and he’s going to have to make sure he doesn’t make very many more between now and then, otherwise he’s just likely to reinforce the doubts that some Republicans seem to have developed during September’s month of debates.
As I noted this morning, this is what happens with a candidate who enters the race late. There’s much less of a margin for error, and much less time to bounce back from an inevitable setback (nobody has ever run a perfect, error-free campaign for President). Perry entered the race in August and immediately became a star mostly because of the reputation he’d developed over the the past couple years among the Tea Party crowd and movement conservatives. When he actually got on the national stage and appeared to have feet of clay, some of that support drifted away as people began to have second thoughts. There’s still time for him to repair the damage, of course, but not as much as there would have been if he’d gotten into the race in May or June.
This is why people sitting on the sidelines like Chris Christie and Sarah Palin would do well to think hard before jumping in the ring. You’re taking a massive risk, you’re going to make some mistakes along the way, and first impressions are hard to correct (just ask Sarah Palin). With the first votes of the 2012 race likely to take place as little as three months from today, the idea that even someone that has had a lot of media exposure over the years can just jump in the race and expect everything to go easily is simply absurd. It’s too late.
